Medidas De Triangulos Que No Se Pueden Construir
A Se pueden construir triángulos con las medidas de los lados indicados en cada renglón. La suma de los 2 lados de los triángulos debe ser mayor al tercer lado en caso contrario no se podrá construir nuestro triangulo.
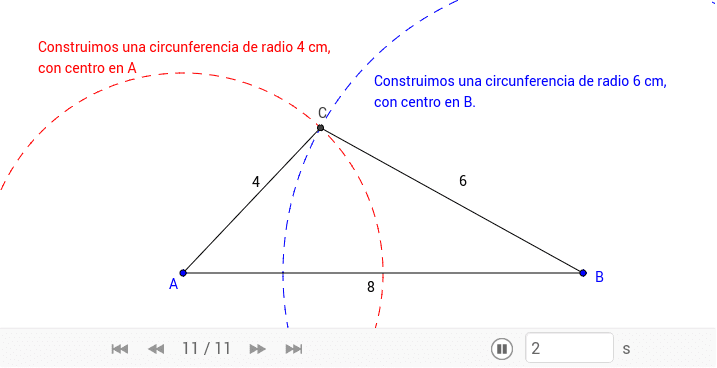
Construccion De Triangulos Geogebra
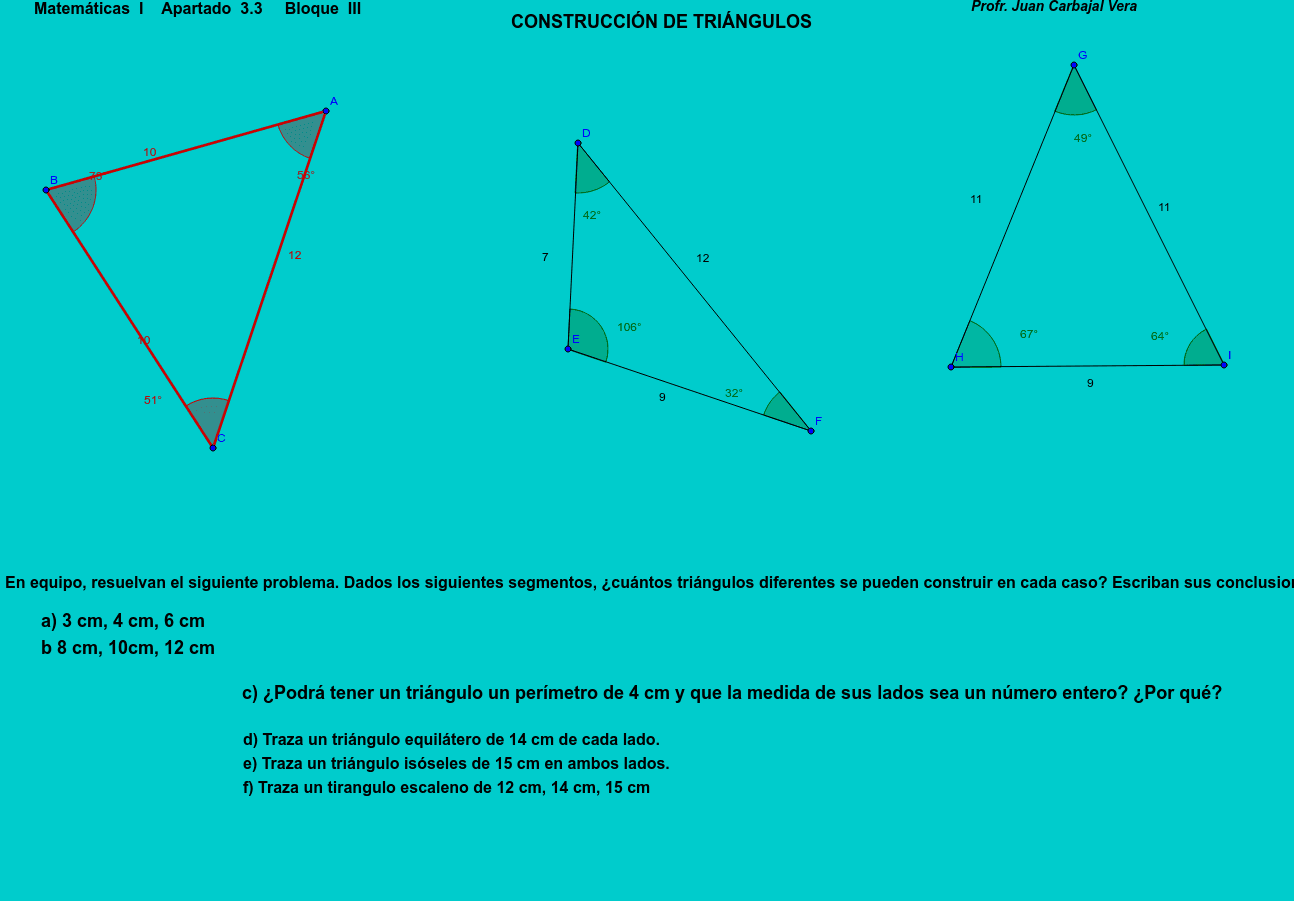
Necesitamos tres datos para construir un triángulo y el ejercicio más básico sería el de construir un triángulo conociendo sus tres lados.

Medidas de triangulos que no se pueden construir. Con la herramienta activada pulsamos sobre los dos puntos que van a a formar un lado y se nos abre una ventana que nos pide el número de vértices 3 en nuestro caso y se nos dibuja el triángulo que podemos personalizar. B En los casos en que sea posible realizar la construcción háganla con regla y compás. Por último clasifiquen los triángulos que dibujaron en acutángulo rectángulo u obtusángulo.
Determinar si las medidas de tres lados forman un triángulo es más fácil de lo que parece. Sea ab y c las medidas de las longitudes de un triangulo se tiene que abc bca acb. 1-En ninguno de estos casos se puede hacer un triángulo.
Dos ejemplos diferentes donde no se pueda construir un triangulo. La suma de los 2 lados de los triangulos debe ser mayor al tercer lado en caso contrario no se podra construir nuestro triangulo. Entonces ahora esto nos conduce a estudiar una propiedad de los triangulos que dice que.
La suma de los 2 lados de los triangulos debe ser mayor al tercer lado en caso contrario no se podra construir nuestro triangulo. Color trazo sombreado medidas etc. Por eso la realidad física que nos rodea grúas y puentes sin ir más lejos está llena de ellos porque para conseguir una estructura que no se mueva es necesario construir triángulos dentro de ella.
D Si se conocen las medidas de dos lados se puede construir un único triángulo. José Villibaldo Pintor Montaño a las 1004. Son de distinta medida los segmentos entre si.
Sea ab y c las medidas de las longitudes de un triangulo se tiene que abc bca acb. Lo que no se vale es por ejemplo dibujar en el pizarrón un triángulo que se vea equilátero y ponerle tres medidas muy distintas a sus lados por descuido sin una intención didáctica. AB BC CA No hay forma de crear un triangulo.
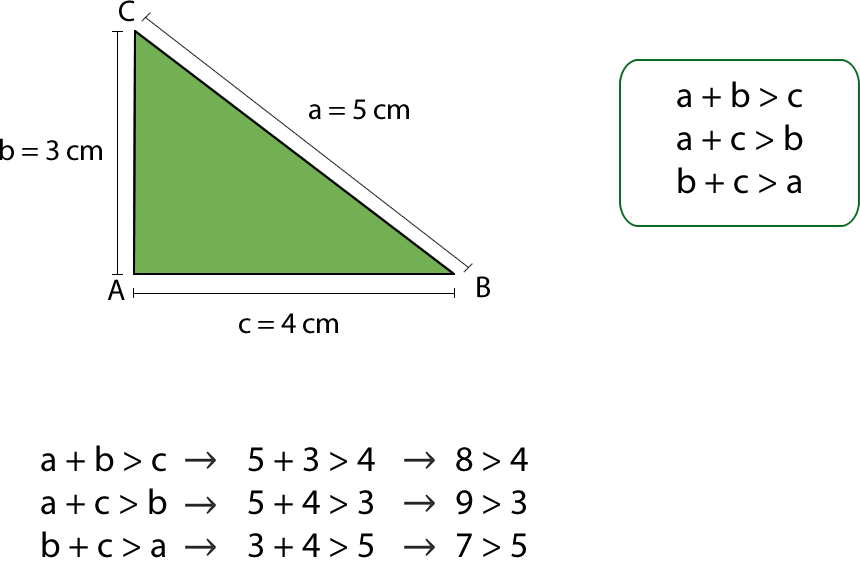
Los datos con los que partimos son. O peor aún ponerle tres medidas que no correspondan a un triángulo que sí se pueda construir recuerden que la suma de las longitudes de los dos lados menores debe ser mayor que la longitud del lado mayor para. Para construir un triángulo según las medidas de sus lados se debe cumplir que la suma de las medidas de dos lados de un triángulo debe ser mayor a la del tercer lado.
Los tres lados a b y c de un triángulo cualquiera y tenemos que. 2-Se puede unicamente en la letra A pero no en la letra B. Lo único que debes hacer es usar el teorema de la desigualdad del triángulo el cual establece que la suma de dos lados del triángulo siempre es mayor que la medida del tercer lado.
Dos de ellos exceden al tercero. Para ello anoten la cualidad de cada ángulo agudo recto u. Calcular la distancia entre A y B.
Podéis encontrar más referencias a los triángulos en el tema 31. Siempre es posible que con los segmentos dados se forme un triángulo. Cuáles son las razones por la que consideras que en ocaciones no se forma un triángulo con los segmentos dados.
Para hallar la distancia entre dos puntos A y B en las márgenes opuestas de un río un ingeniero traza un segmento de recta AC de 240 yardas de longitud junto a una de las márgenes y determina que las medidas de BAC y ACB son 63 20 y 54 10 respectivamente. No siempre es posible construir un triángulo cuando se dan tres medidas de los lados por ejemplo no existe un triángulo cuyos lados midan 7cm 4 cm y 2 cm Para que el triángulo exista cada uno de los lados debe ser menor que la suma de los otros dos. Cuando la suma de dos segmentos es igual o menor al otro segmento no podrá construirse el triángulo.
3-ºLa propiedad de todo triángulo es la suma de las longitudes de dos de sus lados es siempre mayor que la longitud del tercer lado. 3-Julieta construyó un triángulo con un lado de 8 cm y otro lado de 5 cm y dice que se pueden construir muchos triángulos distintos con esos datos. Además si no llegan a la conclusión de comparar las medidas de los lados el maestro puede sugerirlo a fin de que concluyan que la suma de dos lados debe ser mayor que el tercero para que se forme el triángulo.
Para que el triángulo exista cada uno de los lados debe ser menor que la suma de los otros dos. Si empleamos un metro de carpintero para construir difirentes figuras poligonales podemos apreciar que sólo el triángulo es indeformable. Se trazo un ángulo dada su amplitud con una amplitud de 90º colocando el punto A y después B de derecha a izquierda con sentido anti horario para que el ángulo de 90º grados nos quedara de el lado izquierdo en la parte inferior pero no importa en donde se situé el ángulo de 90º grados para que sea rectángulo se puede colocar donde uno guste.
Si esto resulta ser verdad para todas las tres combinaciones de las. Si se esquematiza la propiedad y a los lados del triángulo se les da un valor a b y c se sabe que. Inventá las medidas de tres segmentos AB AC y BC de manera que con ellos.
Se espera que los alumnos se den cuenta de que dadas tres medidas no siempre es posible construir un triángulo cuyos lados tengan precisamente esas medidas. Entonces ahora esto nos conduce a estudiar una propiedad de los triangulos que dice que. E Si se conocen las medidas de los tres ángulos a veces no se puede construir.
No se pueda armar un triángulo ABC. Cuáles son las medidas de los segmentos a b y c. Esto se conoce como desigualdad triangular.
A partir de lo explorado en las actividades 10 11 y. No siempre es posible construir un triángulo cuando se dan tres medidas de los lados por ejemplo no existe un triángulo cuyos lados midan 7cm 4 cm y 2 cm. Existe una fórmula que se aplica a las medidas del trianguloque dice.
R- Se puede ya que cualquier alternativa sirve. Es decir se trabaja en torno de la existencia o no existencia de la solución de un problema. Existe una propiedad conocida como la desigualdad triangular la cual explica.

Propiedades De Los Triangulos Euclides

De Triangulos De Figuras Planas Ppt Video Online Descargar
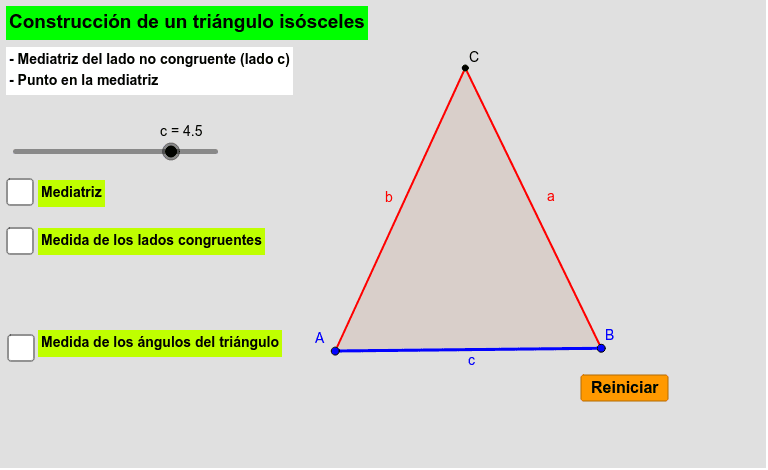
Construccion Geometrica De Triangulo Rectangulo Triangulo Isosceles Y Triangulo Equilatero Geogebra
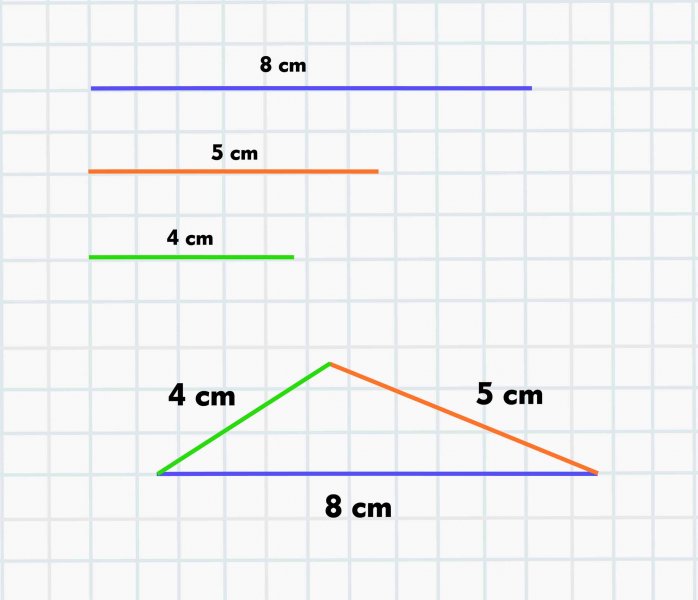
Todavia No Sabes Que Es La Propiedad De Existencia Del Triangulo

Como Trazar Un Triangulo Dados El Lado A Y Los Angulos Adyacentes B Y C Trazado De Triangulos Youtube

Demostraciones Acerca De Triangulos Isosceles Video Khan Academy
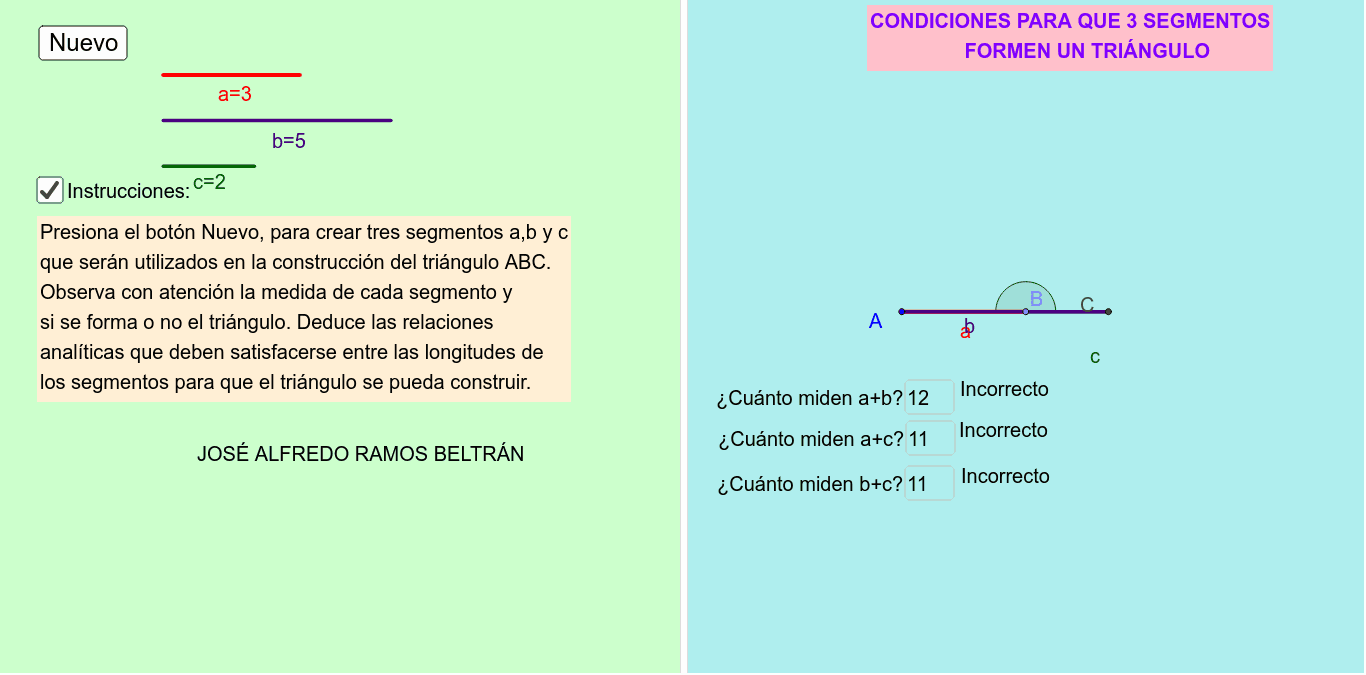
Condiciones Para Que Tres Segmentos Formen Un Triangulo Geogebra

De Triangulos De Figuras Planas Ppt Video Online Descargar
Matematicas Libro Para El Maestro Telesecundaria Primer Grado Volumen Ii

Jugando Con Problemas Matematicos Los Triangulos Enteros

Construccion De Triangulos Youtube

Como Saber Si Hay Un Triangulo Teniendo Las Medidas De Tres Lados
Matematicas Libro Para El Maestro Telesecundaria Primer Grado Volumen Ii

Construccion De Triangulos Segun La Medida De Sus Lados Super Facil Para Principiantes Youtube
Construccion De Triangulos Geogebra

Como Saber Si Se Puede Construir Un Triangulo Propiedad Triangular Youtube





Posting Komentar untuk "Medidas De Triangulos Que No Se Pueden Construir"